プログラミングをやってみようということで最近pythonをいじってるんだけど、三角関数や指数関数の描画、簡単な行列の四則演算には飽きた。
そんなわけでなにかないかと探したところ、線形回帰というのがあったのでコードを丸パ...インスパイヤしてフィボナッチ数列もどきを三次関数で線形回帰してみた。
参考にしたサイト様：
（正直多項式近似の原理部分は僕には難しくて理解できなかったので、今度気が向いたら挑戦したい
またフィボナッチ数列ではなく"もどき"なのはそのままだと僕の技術ではエラーが出てしまったため）
今回解析したのは横軸ｘが[1,2,3,5,8,13,21,34,55]で、
縦軸tが[0,1,2,3,4,5,6,7,8]をとる点の集合。
これを描画すると図1のようになった。
図1.すごい対数関数っぽい
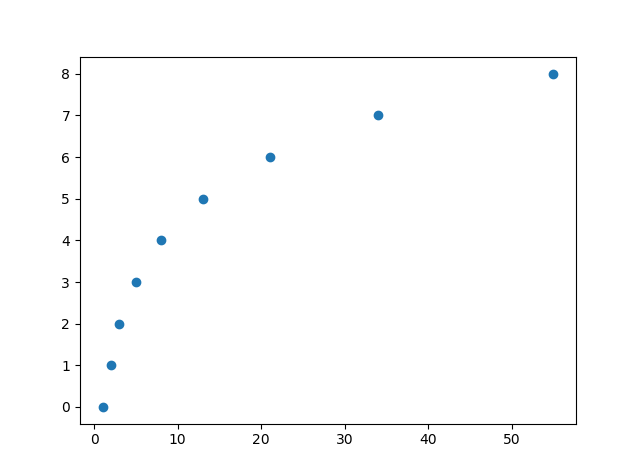
これを三次関数で回帰分析してみると図2のようになった。
図2.回帰分析したもの（→おそらく間違い）
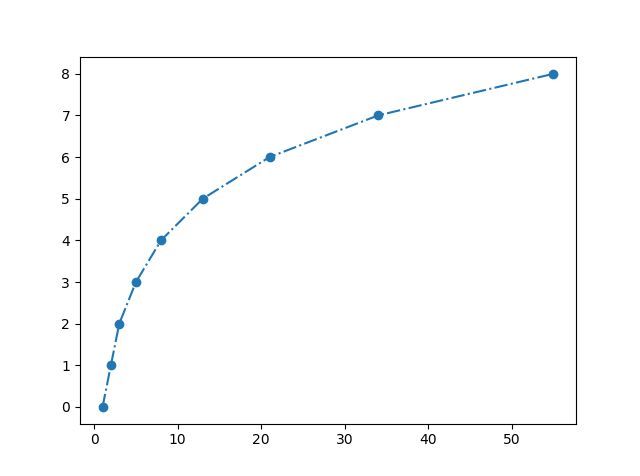
この三次関数の式を出してみると
t=7.72898760*10^(-1)+3.35161447*10^(-1)*x+(-3.76843592)*10^(-3)*x^2+
(-4.87989444)*10^(-7))*x^3
となった。(見づらくて申し訳ない）
追記
もう一回プログラムを走らせたところ図3のようになっていた。
図3.まあそうなるよねという回帰曲線
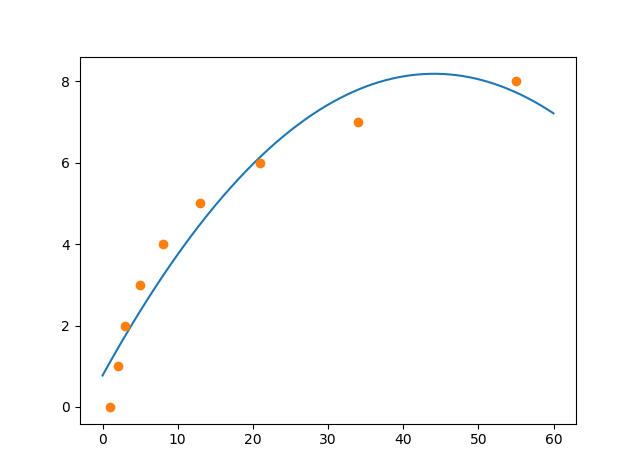
よくよく考えれば、たかが三次関数の回帰分析で点をぴったり通過するのはおかしいので、この回帰が正しいと考えられる。（図2はたぶん設定で点同士をつないでいただけ）
９個の点でこれくらいなのであんまり精度としては高くないと思われる。（そもそも次のXの点でtが落ちることはないし）
（サイトの方の回帰分析は結構うまくいってた気がする）
三次関数の式は上記のものと一緒です。
